| Aktuell |
|---|
|
21. Oktober 2009: - 3D-Animation 20. Oktober 2009: - IP-Ortung Websurfer 28. März 2008: - Erklärung ergänzt 23. Januar 2005: - deutlich schneller 8. Juni 2004: - 3D-Ansicht 5. Juni 2004: - Seite geht online |
besuchen sie auch
mondphase.stephan-brumme.com
mondphase.stephan-brumme.com
| Bildgröße: | 150x75 | 256x128 | 512x256 | 800x400 | 1024x512 | 1536x768 | Darstellung: | 2D | 3D |
|
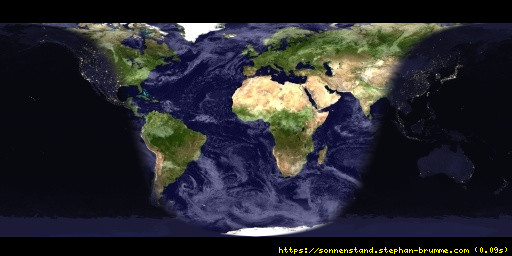
Die angezeigte Grafik wurde soeben neu berechnet und spiegelt den derzeitigen Stand der Sonne wider.
Die momentane Greenwich Mean Time ist 18:55 Uhr am 12.März 2026, das entspricht 19:55 Uhr in Mitteleuropa.
Ihr Computer (IP: 216.73.216.42) scheint sich nahe Arcadia/USA zu befinden.
Als ungefähre Koordinaten wurde 34.1° N, 118.0° W ermittelt.
Die momentane Greenwich Mean Time ist 18:55 Uhr am 12.März 2026, das entspricht 19:55 Uhr in Mitteleuropa.
Ihr Computer (IP: 216.73.216.42) scheint sich nahe Arcadia/USA zu befinden.
Als ungefähre Koordinaten wurde 34.1° N, 118.0° W ermittelt.
|
Kurze Erklärung Zur Berechnung sind zwei Informationen wesentlich: 1. Der aktuelle Tag bestimmt die Neigung der Erde gegenüber der Sonne und damit den Breitengrad, wo die Sonne im Zenit steht. Zum europäischen Sommeranfang ist dies der nördliche Wendekreis und zum hiesigen Winteranfang der südliche Wendekreis (auf der Südhalbkugel sind die Jahreszeiten natürlich vertauscht). Jeweils zum Frühlings- und zum Herbstanfang steht die Sonne senkrecht über dem Äquator. 2. Aus der momentanen Uhrzeit kann man die Rotation der Erde ableiten, was dem Längengrad entspricht. Um 12 Uhr mittags nach Greenwich-Uhrzeit befindet sich die Sonne auf dem Längengrad von Greenwich (bei London) in der Mitte der Grafik. Sie wandert dann im Laufe von 24 Stunden nach ganz links, also westlich, um dann im Osten ganz rechts wieder aufzutauchen und schließlich Greenwich erneut zu erreichen. Wenn Längen- und Breitengrad bekannt sind, über denen die Sonne gerade im Zenit steht, dann erfolgt die virtuelle Beleuchtung der Erde. Dazu wird die Erde als perfekte Kugel betrachtet und der Abstand zur Sonne als unendlich angenommen. Für jeden Punkt auf der Erdoberfläche erhält man aus dessen Längen-/Breitengrad und der Position der Sonne den Einfallswinkel. Dieser bestimmt per Kosinus die Helligkeit in der Grafik in Analogie zur Phong-Beleuchtung. Hinweis Ich erhebe nicht den Anspruch, astronomisch korrekt zu sein. Diese Webseite muss gewisse Vereinfachungen annehmen, um die Berechnungen auf ein erträgliches Maß zu reduzieren. Meine Zielsetzung liegt bei etwa einer Sekunde für die volle Auflösung von 800x400 im 2D-Modus, also über eine Viertelmillion Pixel pro Sekunde. Die 3D-Ansicht bedient sich zur Visualisierung des Raytracings, was wesentlich mehr Aufwand erfordert und deshalb bei gleicher Auflösung ungefähr um Faktor 4 langsamer ist. Technisch wurde das Ganze mit etwa 1000 Zeilen PHP realisiert. |
© 2004 - 2026 Stephan Brumme.
Alle Rechte vorbehalten.
Das verwendete Kartenmaterial stammt von der NASA.
Das verwendete Kartenmaterial stammt von der NASA.